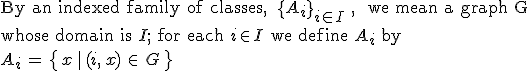집합론에서 ordered pairs의 집합(클래스)를 그래프라고 부른다. 즉, U x V 의 임의의 subclass를 그래프라고 한다. 그래프는 관계표현에 편리하며 몇가지 재미있는 속성과 연산을 가지며 정의역과 치역의 개념을 가진다.

the domain of G : the class of all "first components" of elments of G

the range of G : the class of all "second components" of elements of G

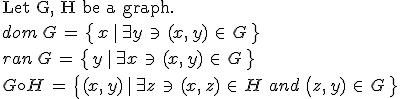
(요거는, y exists such that G has element, (x,y) 라고 읽는다)

Indexed family는 사실 매우 어려운 개념이다. 왜냐하면 index set이 finite set 이 아닐수 있을뿐만 아니라, countable 하지도 않을수 있기 때문이다. 셀수도 없는 집합을 이용하여 index(첨수?)를 한다. 어렵다. -_-;;;

Indexed family 는 집합을 또 다른 집합과 관계지어 만든다. 이때 이렇게 해서 만들어진 집합을 family((indexed family of set ) 혹은 collection이라고 하고 첨수를 매기는데 쓰이는 집합(index를 하는데 쓰이는 집합)을 index set라고 한다. 여기서 indexed family의 원소를 나타내는데 그래프가 유용하게 사용된다. Pinter의 집합론에 다음과 같은 정의(Indexed family of classes의 formal definition라고 나와있다)와 예가 나와있다.