-
방정식의 근 : 대수적 방법과 Iterative Method
방정식(Equation) 으로부터 근을 구할때 ‘근의 공식’등이 존재하는 경우 일반해가 있다고 하는데, 이러한 해를 대수적 해라고 한다. 만일 대수적인 해가 존재할 경우 근을 구하는 방식은 매우 쉽다. - 단지 공식에 넣으면 된다!
Iterative Method 는 근을 구하는 또 다른 방법이다. 이 방법은 근에 근접하는 값을 만들어내는 알고리듬이 있고 이 알고리듬을 반복하여 근과의 차이 (tolerrence 혹은 error)가 얼마 이하가 되면 반복을 멈추어 근을 구하는 방법이다. 유명한 Iterative Method 중에는 Newton-Raphson 방법이 있고 Gauss-Seidel Method의 모티브가 되는 Simple Fixed-point Iteration Method가 있다.
-
Simple Fixed-point Iteration Method
Simple Fixed-point Iteration Method는 개념이 사실 단순하다.
f(x) = 0
이라는 방정식의 근을 구한다고 하자. 위의 방정식 양변에 x를 더하여 f(x) + x = x 라는 새로운 식을 만들고 g(x) = f(x) + x 라고 하면 우리가 구하는 식은
g(x) = x
라는 식의 방정식이고 이것은 그래프적으로
y = g(x)라는 그래프와 y = x 라는 그래프의 교점
임을 알수 있다.
예를들어, f(x) = sqrt(x) - x = 0 을 구하는게 원래 목적이었다면 g(x) = sqrt(x)라고 하고 g(x) = x의 해를 구하는것과 f(x) = 0 의 해를 구하는게 같음을 알 수 있다.
이제부터가 이 방법의 재미난 점인데, x(i+1) = g( x(i) ) 라고 하고 i를 증가하면 x(i+1)이 y=g(x)와 y=x의 교점에 다가감을 알수 있다.
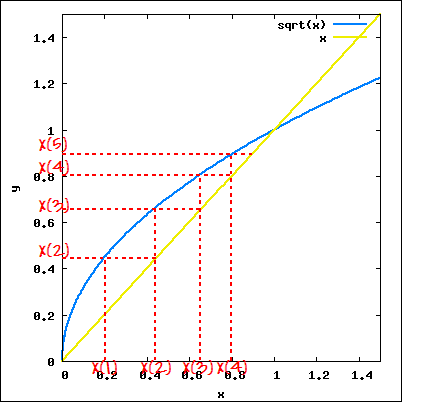
(원래 그래프 자료가 있었는데 유실되었어요 ㅠㅠ 자료 찾음!)
| 그리하여 x의 sequence가 Cauchy Criterion을 만족하면 (즉 어떤 i 가 있어서 | x(i+1) - x(i) | < tolerance) 그때의 x(i+1)를 해라고 할수 있게 된다. |
위 내용을 Octave(matlab) 코드로 짜보면 다음과 같다.
g = inline( 'sqrt(x)', 'x' );
tol = 1.0e-7;
i = 1;
x(i) = 0.2;
while true
x(i+1) = g( x(i) );
if( abs(x(i+1) - x(i)) < tol )
break;
end
i = i + 1;
end
i, x(i+1)
그러면, 24번만에 해를 도출해 낸걸 알수 있다 (i=24, ans=1.0000 뭐 이런 비슷한 값을 출력한다.)
| 물론 항상 해에 접근하는것은 아니고 ‘수렴조건’이 있는데, 그것은 | g’(x) | < 1 이다. |
-
Gauss-Seidel Method
Gauss-Seidel Method는 Simple Fixed-point 방법과 매우 유사하다. 다른 점은 방정식이
1. multicomponent 인 경우
2. linear system 인 경우
인데, 간단히 말하면 ‘연립 일차방정식’의 경우에 해를 ‘반복적’으로 구하는 방법이다.
Applied Numerical Methods with MATLAB 이라는 책에 있는 예제인
3x - 0.1y - 0.2z = 7.85
0.1x - 7y - 0.3z = -19.3
0.3x - 0.2y + 10z = 71.4
의 해를 Gauss-Seidel Method로 구하는 matlab 코드를 보면,
% from 3x - 0.1y - 0.2z = 7.85
% x = (7.85 + 0.1y + 0.2z)/3
f = inline('(7.85 + 0.1*y + 0.2*z)/3', 'y', 'z');
% from 0.1x - 7y - 0.3z = -19.3
% y = (-19.3 - 0.1x + 0.3z)/7
g = inline('(-19.3 - 0.1*x + 0.3*z)/7', 'x', 'z');
% from 0.3x - 0.2y + 10z = 71.4
% z = (71.4 - 0.3x + 0.2y)/10
h = inline('(71.4 - 0.3*x + 0.2*y)/10', 'x', 'y');
i = 1;
tol = 1.0e-7;
x(i)=0; y(i)=0; z(i)=0;
while true
x(i+1) = f( y(i), z(i) );
y(i+1) = g( x(i+1), z(i) );
z(i+1) = h( x(i+1), y(i+1) );
if( abs(max( [x(i+1)-x(i) y(i+1)-y(i) z(i+1)-z(i)] )) < tol )
break;
end
i = i + 1;
end
i, x=x(i+1), y=y(i+1), z=z(i+1)
만일
x(i+1) = f( y(i), z(i) );
y(i+1) = g( x(i+1), z(i) );
z(i+1) = h( x(i+1), y(i+1) );
부분이
x(i+1) = f( y(i), z(i) );
y(i+1) = g( x(i), z(i) );
z(i+1) = h( x(i), y(i) );
가 되면, 즉 현재 루프에서 적용된것값을 적용되자마자 써먹는게 아니고 루프를 다 돌고 사용한다면, 그 방법을 Jacobi iterative method 라고 한다.
Simple fixed-point iterative method처럼 Gauss-Seidel도 수렴조건이 있는데, 연립일차 방정식을 matrix로 나타냈을때 그 matrix가 ‘diagonal dominant’ 하면 된다.